The Reciprocal Of 20 Is

In Maths, reciprocal is but divers as the inverse of a value or a number. If n is a real number, then its reciprocal will be 1/n. Information technology means that we take to convert the number to the upside-downwardly form. For example, the reciprocal of 9 is 1 divided by 9, i.eastward. one/ix. Now, if we multiply a number by its reciprocal, it gives a value equal to 1. It is also called multiplicative inverse .

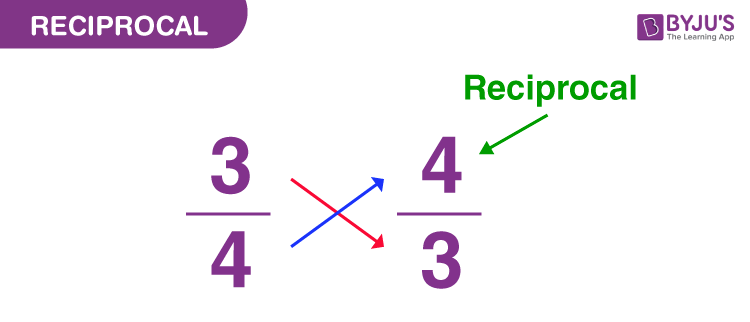
Reciprocal

The give-and-take reciprocal came from the Latin give-and-take "reciprocus" meaning "returning". Hence, information technology returns its original value, if nosotros take the reciprocal of an inverted number. In this commodity, we are going to learn the definition of reciprocal, how to notice the reciprocal of numbers, fractions and decimals with many examples.

Table of Contents:

- Definition
- Reciprocal of a Number
- Reciprocal of a Negative Number
- Reciprocal of a Fraction
- Reciprocal of a Mixed Fraction
- Reciprocal of a Decimal
- Finding Unity
- Application of Reciprocal
- Rules for Reciprocal
- Examples
- Do Questions
- FAQs

Definition

In Mathematics, the reciprocal of whatever quantity is, one divided by that quantity. For any number 'a', the reciprocal will be one/a. If the given number is multiplied by its reciprocal, nosotros go the value 1.

Case: Reciprocal of a number 7 is i/seven.

Thus, if we multiply 7 and i/vii, we get 1.

I.e., 7 × (1/7) = ane

Other Definitions of Reciprocal

It has many other definitions too :

It is too chosen the multiplicative inverse .
It is similar to turning the number upside downwardly.
It is also found byinterchanging the numerator and denominator.
All the numbers take reciprocal except 0.
The product of a number and its reciprocal is equal to 1.
More often than not, reciprocal is written every bit, 1/x or x^-1 for a number x.

Instance: The reciprocals of 3 and 8 are i/3 and 1 /8.

Information technology is also expressed past the number raised to the power of negative ane and tin exist plant for fractions and decimal numbers too.

In maths, when you have the reciprocal twice, you will get the same number that you started with.

Example: The reciprocal of four is 1/4. When you repeat this step it becomes 4/1 or 4.

Thus, you get the same number where you started with.

Non For Zero

We cannot apply the reciprocal condition on zero, since information technology volition render an indefinite value.

1/0 = Undefined

Therefore, nosotros tin have a reciprocal for all real numbers just not for zero.

Reciprocal of a Number

It is defined as one over that number. In other words, the reciprocal of a number is defined every bit the one divided by the given number.

Example: Notice the reciprocal of five

Solution: To find the solution, we volition employ ten = one/x

Therefore, 5= 1/v

The reciprocal of a function, f(x) = f(i/ten)

Reciprocal of Negative Numbers

For whatever negative number -x, the reciprocal can be institute by writing the inverse of the given number with a minus sign forth with that (i.e) -1/x. For case, the reciprocal of – 4x ² is written as -one/4x ^two . Go through the following steps to find the reciprocal of the negative number.

Pace ane: For whatsoever negative number, write the given number in the grade of an improper fraction past writing the number i in the denominator.

Step 2: Now, interchange the numerator and denominator values.

Step 3: Add a minus sign (-) to the resultant number.

Now, Consider a negative number, -17.

Footstep 1: Convert the number 17 in the improper fraction. (i.east) 17/ane.

Stride 2: Interchanging the numerator and denominator value, we get ane/17.

Step three: Finally, adding a negative sign to the resultant number, we get -1/17.

Therefore, the reciprocal of -17 is -1/17.

Reciprocal of a Fraction

The reciprocal of a fraction tin exist found past interchanging the numerator and the denominator values.

Example: Find the reciprocal of 2 / 3

Solution: To discover the solution we will follow the following steps

The reciprocal of two/3 is iii/2. (or)

Use the formula, x = one/x,

Here, x = ii/three

Thus, x = 1 / x = i / (2/three)

= 3/2

Therefore, the reciprocal of a fraction 2/three is 3/two.

Reciprocal of a Mixed Fraction

In order to find the same for a mixed fraction, catechumen it into improper fractions and perform the operation.

Consider a mixed fraction, 4(1/ii).

The outset footstep is to catechumen a mixed fraction into an improper fraction.

4(1/ii) = 9/2

At present, you get the fraction and do the same operation for finding the reciprocal by flipping the numerator and the denominator.

Therefore, the solution for 9/2 is 2/nine.

Reciprocal of a Decimal

The reciprocal of a decimal is the same every bit information technology is for a number divers by 1 over the number.

Example:

Notice the reciprocal of a decimal 0.75

Solution:

The reciprocal of a number, x = 1/x

Therefore, 0.75= ane/0.75

An alternate method to find it is given beneath.

Consider the same example, 0.75.

Commencement, yous take to check whether the given decimal number is possible for converting into a fractional number. Hither 0.75 is written as three/4

At present, find the reciprocal of iii/4 which gives 4/three

When y'all verify both the solutions, it results in the same.

That is, 1/0.75 = 1.33 and

four/3 = 1.33

Finding Unity

If nosotros multiply the reciprocal of a number by the number itself, nosotros volition get the value equal to unity (1). Let us see some examples hither:

2 × (1/two) = 1
3 × (one/3) = 1
10 × (ane/10) = i
50 × (i/fifty) = 1
100 × (1/100) = i

From the to a higher place examples, nosotros can see that the multiplication of a number to its reciprocal gives 1. Hence, we can say that the number is multiplied by its reciprocal, nosotros go 1.

Application of Reciprocal

The most important application of reciprocal is used in division operation for fractions. If we desire to divide the first fraction past the second fraction, the outcome tin can be found by multiplying the first fraction with the reciprocal of the second fraction.

For case, (2/5) ÷ (7/five)

Here, the first fraction is 2/5

The second fraction is 7/5

Thus, the reciprocal of the 2d fraction is 5/7

Hence, (two/5) ÷ (7/five) = (2/5) × (five/7)

(2/five) ÷ (7/5) = 2/seven.

Rules for Reciprocal

The 2 important rules for reciprocal are:

For a number x, the reciprocal volition exist one/ten or also can exist written as x^-1. For instance, if 7 is the number, then the reciprocal will exist one/seven.
For a fraction x/y, the reciprocal volition be y/x. For example, if 3/5 is the given fraction, then its reciprocal will exist 5/3.

Solved Examples

Go through the below examples:

Case 1:

Find the reciprocal of 2 and nine

Solution:

Given that, the ii integers are 2 and nine

Therefore, the reciprocal of two is ane/two

The reciprocal of ix is 1/9

Example ii:

Make up one's mind the reciprocal of 3 / (2/3)

Solution:

Given number three/(⅔) is a fraction.

3 / (2/3) can be written as ix/2

i.e., three/(⅔) = nine/2

Hence, the reciprocal of 9/ii is 2/ix.

Case 3:

Find the reciprocal of -v/iv

Solution:

Given fraction is -5/4

The reciprocal of -5/4 is -iv/5.

Instance iv:

Find the reciprocal of the decimal 0.25.

Solution:

Given decimal number = 0.25.

Hence, the reciprocal of 0.25 is 1/0.25.

Alternate method:

The fraction equivalent to the decimal number 0.25 is i/4.

Hence, the reciprocal of ¼ is four/1.

Verification:

The resultant number obtained from both methods will result in the aforementioned value.

(i.eastward.) 1/0.24 = iv or 4/1.

Example 5:

Find the reciprocal of the negative number -45.

Solution:

Given that the negative number is -45.

Hence, the reciprocal of -45 is -1/45.

Exercise Questions on Reciprocals

Discover the reciprocal for the following numbers:

29
xiv/15
1.25
-80
ax ²

Oft Asked Questions on Reciprocal

Define reciprocal.

The reciprocal is defined as the multiplicative inverse of a number. In other words, the reciprocal of a number is defined as 1 divided by that number. The product of a given number and its reciprocal volition always give the value ane.

How to determine the reciprocal of a fraction?

The reciprocal of a fraction can be determined by interchanging the values of the numerator and denominator. For example, ¾ is a fraction. The reciprocal of ¾ is iv/3.

How to determine the reciprocal of the mixed fraction?

To discover the reciprocal of the mixed fraction, first, convert the mixed fraction into the improper fraction, and so accept the reciprocal of the improper fraction. For example, 2 ¾ is a mixed fraction. When information technology is converted to an improper fraction, we get 11/4. Hence, the reciprocal of 11/4 is 4/11.

What is the reciprocal of 0?

The number zero (0) does not have a reciprocal. Because, if any reciprocal number is multiplied past 0, it volition not give the product as 1. It will result in zero.

What is the reciprocal of infinity?

The reciprocal of infinity is ane/∞, which is equal to zero. It means that 1/∞=0. Information technology is noted that the reciprocal of infinity is zero exactly, which means not infinitesimal.

For more information on finding reciprocals and other Maths concepts, visit BYJU'S – The Learning App and also get various Maths related videos to understand the concept in an easy and engaging way.