1.01 As A Mixed Number

10.2.1.1: Introduction to Fractions and Mixed Numbers

Final updated
Relieve as PDF

Page ID: 30873

Learning Objectives

Identify the numerator and denominator of a fraction.
Represent a fraction equally part of a whole or role of a set.

Introduction

Many problems in mathematics deal with whole numbers, which are used to count whole units of things. For example, you can count students in a classroom and the number of dollar bills. You lot demand other kinds of numbers to describe units that are not whole. For example, an aquarium might be partly full. A group may accept a meeting, simply merely some of the members are nowadays.

Fractions are numbers used to refer to a function of a whole. This includes measurements that cannot be written as whole numbers. For case, the width of a piece of notebook newspaper is more than viii inches but less than nine inches. The part longer than 8 inches is written equally a fraction. Here, you lot volition investigate how fractions can be written and used to stand for quantities that are parts of the whole.

Identifying Numerators and Denominators

A whole can be divided into parts of equal size. In the example beneath, a rectangle has been divided into 8 equal squares. Four of these viii squares are shaded.

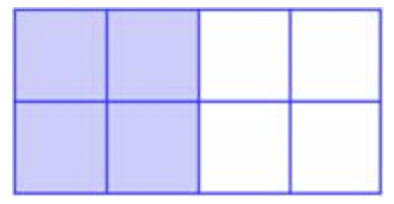
$Screen Shot 2021-04-17 at 12.37.35 PM.png$

The shaded area can be represented by a fraction. A fraction is written vertically every bit two numbers with a line between them.

The denominator (the bottom number) represents the number of equal parts that make upwards the whole. The numerator (the meridian number) describes the number of parts that y'all are describing. Then returning to the example in a higher place, the rectangle has been divided into 8 equal parts, and iv of them take been shaded. Yous can utilize the fraction $\ \frac{4}{8}$ to describe the shaded part of the whole.

In $\ \frac{iv}{viii}$, the four is the numerator and tells how many parts are shaded. The 8 is the denominator and tells how many parts are required to brand the whole.

Parts of a Set

The rectangle model above provides a good, basic introduction to fractions. However, what practice you practice with situations that cannot be every bit hands modeled by shading part of a figure? For instance, think about the following situation:

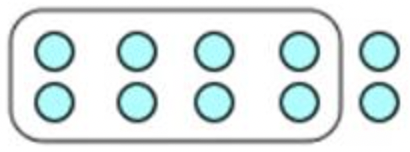
Marc works as a Quality Assurance Managing director at an automotive plant. Every hour, he inspects 10 cars; $\ \frac{iv}{5}$ of those laissez passer inspection.

In this case, 10 cars make upwards the whole grouping. Each car can be represented every bit a circumvolve, every bit shown below.

$Screen Shot 2021-04-17 at 1.07.32 PM.png$

To bear witness $\ \frac{four}{5}$ of the whole group, you outset need to split up the whole group into 5 equal parts. (You know this considering the fraction has a denominator of 5.)

$Screen Shot 2021-04-17 at 1.09.35 PM.png$

To show $\ \frac{4}{5}$, circumvolve 4 of the equal parts.

$Screen Shot 2021-04-17 at 1.10.40 PM.png$

Here is another instance. Imagine that Aneesh is putting together a puzzle made of 12 pieces. At the start, none of the pieces has been put into the puzzle. This means that $\ \frac{0}{12}$ of the puzzle is complete. Aneesh and then puts four pieces together. The puzzle is $\ \frac{4}{12}$ complete. Soon, he adds iv more pieces; 8 out of 12 pieces are now connected. This fraction can be written as $\ \frac{eight}{12}$. Finally, Aneesh adds four more pieces. The puzzle is whole, using all 12 pieces. The fraction can be written every bit $\ \frac{12}{12}$.

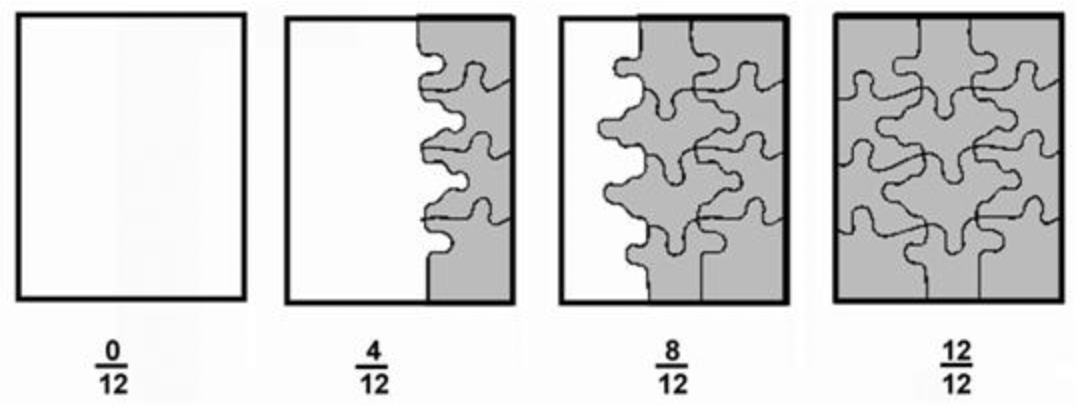
$Screen Shot 2021-04-17 at 1.19.11 PM.png$

Notation that the number in the denominator cannot be nil. The denominator tells how many parts make upwards the whole. So if this number is 0, and then there are no parts and therefore there tin be no whole.

The numerator can be nil, every bit information technology tells how many parts you lot are describing. Discover that in the puzzle instance above, you can utilize the fraction $\ \frac{0}{12}$ to represent the state of the puzzle when 0 pieces take been placed.

Fractions can also be used to clarify data. In the data tabular array below, 3 out of v tosses of a coin came up heads, and ii out of five tosses came up tails. Out of the full number of coin tosses, the portion that was heads tin be written as $\ \frac{3}{5}$. The portion that was tails can be written as $\ \frac{two}{5}$.

Money Toss	Result
1	Heads
2	Tails
three	Heads
4	Heads
5	Tails

Exercise

Sophia, Daphne, and Charlie are all participating in a relay race to raise coin for charity. First, Sophia will run 2 miles. Then, Daphne volition run v miles. Finally, Charlie will terminate the race past running 3 miles. What fraction of the race will Daphne run?

5 miles
$\ \frac{5}{ten}$
$\ \frac{ii}{5}$
$\ \frac{5}{3}$

Reply

Incorrect. Daphne will run 5 miles, but that does not indicate the fractional office of the race that she will run. To find the fraction, get-go find the whole length of the race by combining the distances the three people will run: 2+v+3=10. So consider the altitude Daphne will run. The correct answer is $\ \frac{v}{10}$.
Correct. The entire race is x miles long, and Daphne volition run 5 miles. This means she volition run $\ \frac{five}{10}$ of the race.
Incorrect. To find the fraction, first find the whole length of the race past combining the distances the iii people will run: 2+5+iii=10. And then consider the distance Daphne volition run. The correct reply is $\ \frac{5}{ten}$.
Incorrect. To observe the fraction, offset find the whole length of the race by combining the distances the three people will run: 2+5+3=10. And so consider the distance Daphne volition run. The correct answer is $\ \frac{5}{10}$.

Parts of a Whole

The "parts of a whole" concept can be modeled with pizzas and pizza slices. For case, imagine a pizza is cut into 4 pieces, and someone takes ane piece. At present, $\ \frac{1}{4}$ of the pizza is gone and $\ \frac{3}{four}$ remains. Note that both of these fractions accept a denominator of 4, which refers to the number of slices the whole pizza has been cutting into.

$Screen Shot 2021-04-17 at 2.09.07 PM.png$

Example

Joaquim bakes a blueberry pie for a potluck dinner. The total pie is cut into half dozen equal slices. Subsequently everybody eats dessert, only one slice of the pie remains. What fraction of the pie remains?

Solution

$\ \frac{?}{6}$	The pie was cutting into six equal slices, and then the denominator of the fraction will be 6.
$\ \frac{i}{6}$	Only i slice remains, so the numerator of the fraction will be 1.
	$\ \frac{1}{6}$ of the pie remains.

Example

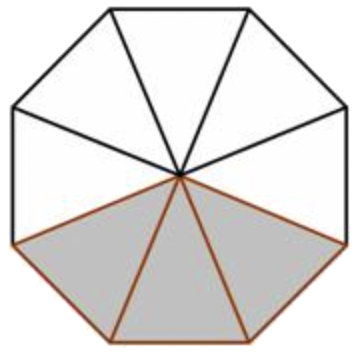$Screen Shot 2021-04-17 at 2.png$ Write a fraction to represent the portion of the octagon that is not shaded.

Solution

$\ \frac{?}{8}$	The octagon has eight equal sections, so the denominator of the fraction will be 8.
$\ \frac{5}{8}$	V sections are non shaded, so the numerator of the fraction volition be 5.
	$\ \frac{v}{8}$ of the octagon is not shaded.

Measurement Contexts

You tin can use a fraction to represent the quantity in a container. This measuring cup is $\ \frac{3}{4}$ filled with a liquid. Annotation that if the loving cup were $\ \frac{iv}{4}$ full, it would exist a whole loving cup.

$Screen Shot 2021-04-17 at 2.33.37 PM.png$

You lot tin as well use fractions in measuring the length, width, or height of something that is not a total unit. Using a 12-inch ruler, you mensurate a shell that is 6 inches long. Y'all know that 12 inches equals one foot. And so, the length of this trounce is $\ \frac{vi}{12}$ of a foot; the 12-inch ruler is the "whole," and the length of the vanquish is the "function."

$Screen Shot 2021-04-17 at 3.01.09 PM.png$

Exercise

$Screen Shot 2021-04-17 at 3.png$

Which fraction represents the portion of the shape that is shaded?

$\ \frac{8}{7}$
$\ \frac{vii}{8}$

Answer

Incorrect. The total number of parts that brand upward the whole, viii, is the denominator. That is the number beneath the fraction bar. The number of shaded parts, seven, is the numerator. That is the number above the fraction bar. The correct answer is $\ \frac{seven}{8}$.
Correct. The total number of parts that brand up the whole, 8, is the denominator (below the fraction bar). The number of shaded parts, 7, is the numerator (higher up the fraction bar).

Summary

Fractions are used to correspond parts of a whole. You can apply fractions when describing substances, quantities, or diagrams that are not complete. You besides use fractions to depict numbers of people or objects that do not make upward a consummate grouping. Fractions are written with a numerator and denominator. The numerator (above the fraction bar) tells the number of parts beingness described, and the denominator (beneath the fraction bar) tells the number of parts that make up the whole.